2023. 3. 27. 11:04ㆍTool
안녕하세요!
ViT를 공부하며 핵심적인 개념인 inductive bias에 대해 추가적으로 공부하게 되었습니다.
An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale에는 inductive bias와 관련해 다음과 같은 구절이 나옵니다.
"Transformers lack some of the inductive biases inherent to CNNs, such as translation equivariance and locality, and therefore do not generalize well when trianed on insufficient amounts of data."(p.1)
"We find that large scale training trumps inductive bias."(p.2)
ViT의 경우, CNN과 비교하였을 때 대용량의 큰 데이터셋으로 pre-training해야 좋은 성능이 나오는 특징을 가지는데요.
이런 특징을 가지는 이유가 inductive bias와 관련이 있습니다.
해당 게시물을 통해 그 궁금증을 풀어보고자 합니다.
01. Bias와 Variance 정의
1.1 실제값, 예측값, 기대값
- f(x): 입력 데이터 x에 대한 실제 정답값. 정답은 1개이기 때문에 f(x)는 1개만 존재
- ^f(x): 입력 데이터 x에 대한 예측값. 모델의 상태에 따라 다양한 값 출력 가능
- E[^f(x)]: ^f(x)들의 평균(기댓값). 대표 예측값

1.2 Bias, Variance, Error 정의
(1) Bias

- Bias? "예측값 - 실제 정답"의 평균. 예측값이 실제 정답값과 얼마나 차이 나는지 확인하는 지표
- 만약, Bias가 크다면 그만큼 예측값과 실제 정답 사이 차이가 크며, 모델이 잘 예측하지 못했음 의미
- Bias가 크게 되면 과소적합(underfitting) 야기
(2) Variance

- Variance? 분산. 다양한 데이터 셋에 대해 예측값이 얼만큼 변화할 수 있는 지에 대한 양(Quality)
- 모델이 얼만큼 flexibiity(유연성) 가지는 지에 대한 의미 or 예측 모델의 복잡도 의미로 사용됨
- 낮은 Variance는 들어오는 데이터에 따라 예측값 크게 바뀌지 않는 것 의미
- 높은 Variance는 들어오는 데이터에 따라 예측값 크게 바뀜 의미
- Variance가 큰 모델은 훈련 데이터에 지나치게 적힙 시켜 과대적합(overfitting) 야기
(3) Error

- Error = bias(x) + variance(x) + *noise(x)
- *noise(x)는 데이터가 본질적으로 가지는 한계치로 irreducible error(줄일 수 없는 에러). bias와 variance를 0으로 만든다고 하더라도 그 모델이 항상 완벽할 수는 없기 때문에 추가된 항
1.3 Bias와 Variance 관계
(1) Bias Variance 관계
- Bias와 Variance는 Trade-off 관계
- Bias는 학습 데이터 교체했을 때 모델의 정확도 어느 정도 차이나는지 관측
- Variance는 특정 데이터에 모델이 얼마나 민감하게 반응하는지 관측
- Bias 높은 경우? 모델이 학습 데이터 특성 충분히 학습하지 않아 underfitting 되었다고 판단
- Variance 높은 경우? 모델이 학습 데이터 특성 너무 세세하게 학습해 overfitting 되었다고 판단
- 가장 이상적인 구간은 Low Variance & Low Bias
- 가운데 위치한 빨간색 원: 실제 예측값(target)
- 파란색 점: 모델에서 예측한 값

| Bias | Variance | 특징 |
| Low Bias | Low Variance | 예측 값들이 정답 근방에 분포되어 있음 예측 값들이 서로 모여 있음 |
| Low Bias | High Variance | 예측 값들이 정답 근방에 분포되어 있음 예측 값들이 서로 흩어져 있음 |
| High Bias | Low Variance | 예측 값들이 정답에서 떨어져 있음 예측 값들이 서로 모여 있음 |
| High Bias | High Variance | 예측 값들이 정답에서 떨어져 있음 예측 값들이 서로 흩어져 있음 |
(2) Bias variance tradeoff of various network structure
- 다중의 inductive bias 갖는 모델을 설계하는 것은 일반적으로 모델의 sample efficiency 증진하는 경향 있음
- 하지만 inductive bias는 동시에 모델을 규제하기 때문에 모델의 표현력 저하한다는 한계 있음
- (왼쪽) 적은 파라미터만을 사용해서 데이터 단순하게 모델링
- Linear Regression? 굉장히 높은 bias 들어간 모델("x와 y 상관 관계가 선형이다"라는 가정 전제로 모델링되었기 때문)
- (오른쪽) 높은 차수 모델 이용하는 경우, high variance가 생김
- (왼쪽) 적은 파라미터만을 사용해서 데이터 단순하게 모델링

02. Inductive Bias
- 머신러닝에서는 target 예측하기 위해 학습할 수 있는 알고리즘, 모델, 제한된 데이터 주어짐
- 학습시, 모델이 너무 학습 데이터에만 맞춤형으로 학습되면 좋지 않음
- 학습데이터가 전체 데이터 대표하기에 부족함이 있을 수 밖에 없음
- 데이터가 풍부하게 많은 경우에는 상관이 없지만, 일반적으로 데이터 적은 경우에도 모델이 올바른 inductive bias 보유하여 일반성(generality) 갖추는 것 중요
- 일반적으로 모델이 갖는 generalization problem에는 2가지가 있음
- Models are brittle(불안정): 데이터 input이 조금만 바뀌어도 모델 결과 달라지는 것
- Models are spurious(겉으로만 그럴싸): 데이터 특성 학습하는 것이 아닌 결과와 편향 학습하는 것(이해는 안 하고 답만 외우는 느낌)
- 이러한 문제점 해결하기 위해 inductive bias 이용
- 학습 데이터 넘어 다른 데이터(검증용, 테스트용 등의 새로운 데이터)에 대해서도 일반화할 수 있는 능력 가진 모델에는 inductive bias 존재한다고 봄
- Inductive bias? Training에서 만나보지 않았던 상황에 대하여 정확한 예측 하기 위해 사용하는 추가적 가정들
- 데이터 특성에 맞는 적절한 inductive bias 가지는 모델 사용해야 높은 성능 기록 가능
- 예를 들어, CNN은 Locality(근접 픽셀끼리 종속성), Transitional Invariance(사물 위치 바뀌어도 동일 사물 인식) 등의 특성을 가지기에 이미지 데이터에 적합한 모델
- 아래 표는 inductive bias 예시
| 예시 | 설명 |
| Translation invariance | 물체의 입력 내 시/공간상 절대적 위치가 함수 출력에 영향 미치지 않음 |
| Translation Equivariance | 물체의 입력 내 시/공간상 절대적 위치가 함수 출력에 영향 미침 |
| Minimum cross-validation error | 다중의 가설 존재할 때, 교차 검증 오차가 낮은 가설 선택해야 함 |
| Maximum margin | 두 클래스 사이에 경계 그릴 때 경계 너비 최대화 해야 함 |
| Minimum description length | 복잡한 현상 설명하는 가설은 보다 짧고 명료할수록 좋음 |
| Minimum features | 유용하다는 근거가 없는 feature의 경우 제거하는 것이 좋음 |
| Low density separation | 분류 모델의 decision boundary는 feature 밀도가 낮은 곳에 위치해야 함 |
| Smoothness assumption | 두 데이터가 입력 공간 상에서 가까운 위치에 위치한다면 출력 공간 상에서 역시 가까워야 함 |
| Cluster assumption | feature space 내 데이터셋에 대해 같은 cluster 내 존재하는 데이터는 같은 클래스 공유할 확률 높음 |
| Ridge regularization | 모델 parameter들이 Gaussian prior에서 추출됨 |
| Lasso regularization | 모델 parameter들이 Laplace prior에서 추출됨 |
03. Inductive biases in image data
CNN 모델을 활용해 학습할 경우, inductive bias를 통해 이미지 다루는 작업에 강점을 가지게 됨
이때, Inductive Bias는 아래와 같이 정의됨(Springer)
"In machine learning, the term inductive bias refers to a set of (explicit or implicit) assumptions made by a learning algorithm in order to perform induction, that is, to generalize a finite set of observation (training data) into a general model of the domain."
3.1 Stationarity in image dataset
- 데이터의 통계적 특징이 시/공간에 대해 불변한다는 가정
- 시계열 데이터? 시간이 지남에 따라 변화하지만 평균과 분산은 일정하게 유지됨

- CNN은 입력 데이터가 대부분의 입력 공간상에서 유사한 통계적 특성 갖는 것 가정함
- receptive field로 나누게 되면, 각 receptive field 내에 존재하는 사람의 수 등의 통계적 특성이 균일하게 유지됨

- 이미지에서 한 특징이 위치와 상관없이 다수 존재할 수 있으며, 어떤 위치에서 학습한 특징 파라미터를 이용해 다른 위치에서도 동일한 특징 추출 가능(Parameter Sharing)
Parameter Sharing
영화 <라붐> 스틸컷 이미지에서 입이라는 특징 추출시, 2개의 입을 하나의 특징으로 취급해 위치와 상관없이 추출
-> 각 local 영역에서 feature 추출하는 필터들 간 파라미터 공유함. 이는 이미지 데이터의 translation invariance/stationarity 특징 활용함
-> Parameter Sharing 사용하면 feature map 1개 출력하기 위해 필터 1장만 유지하기 때문에 FCN보다 훨씬 적은 수의 파라미터 사용
-> 연산량 적어지고 statistical efficiency(상대적으로 더 적은 양의 데이터로도 더 좋은 성능을 내는 것을 측정하는 품질 측정 중 1개) 향상
- 아래 이미지는 영화 라붐의 스틸컷으로, 인물들의 입의 위치가 박스로 표시되어 있음

- 동일한 특징에 해당하는 '입'이 서로 다른 위치에 동시에 2개 존재하는 상황
- 입의 위치, 모양은 조금 다르지만, 동일한 특징이기에 이미지 내에서의 stationarity 특성
3.2 Locality
- 이미지 데이터는 locality(지역성) 특성 지님
- 컴퓨터는 픽셀 단위로 데이터 인지하며 인접한 픽셀끼리는 유사한 값 지님
- 눈 부분에 해당하는 픽셀들은 유사한 모양(shape)와 질감(texture) 지니고 있음

- 입력상의 시공간 상에서 가까운 위치에 위치한 데이터끼리 보다 높은 상관관계 갖는다는 가정
- 인접한 픽셀끼리 더 높은 상관관계 가지며 멀리 떨어진 픽셀끼리는 낮은 상관관계 갖음
- 멀리 떨어진 픽셀끼리는 서로 낮은 상관관계 가짐
- 이는 합성공 신경망이 필터(혹은 local receptive field)가 이동하면서 윈도우 단위로 특성 학습하기 때문
- 동일한 윈도우 간 weight sharing 통해 translation invariance라는 inductive bias 보유하게 됨
- translation invariance? 사물 위치 바뀌더라도 동일한 사물로 인식할 수 있는 특징
- 반면, MLP에서는 동일한 값 가진 input이더라도 위치가 조금이라도 달라지면 벡터값이 아예 달라지기 때문에 translation invariance가 불가능
- CNN에서는 사물 위치가 바뀌더라도 연산 결과의 위치가 윈도우가 참조하는 원본 픽셀들의 위치에 따라 달라지기에 Translation Equivariance 학습
- Translation Equivariance? 개체 위치 변하면 연산의 activation 위치 바뀌는 것 의미
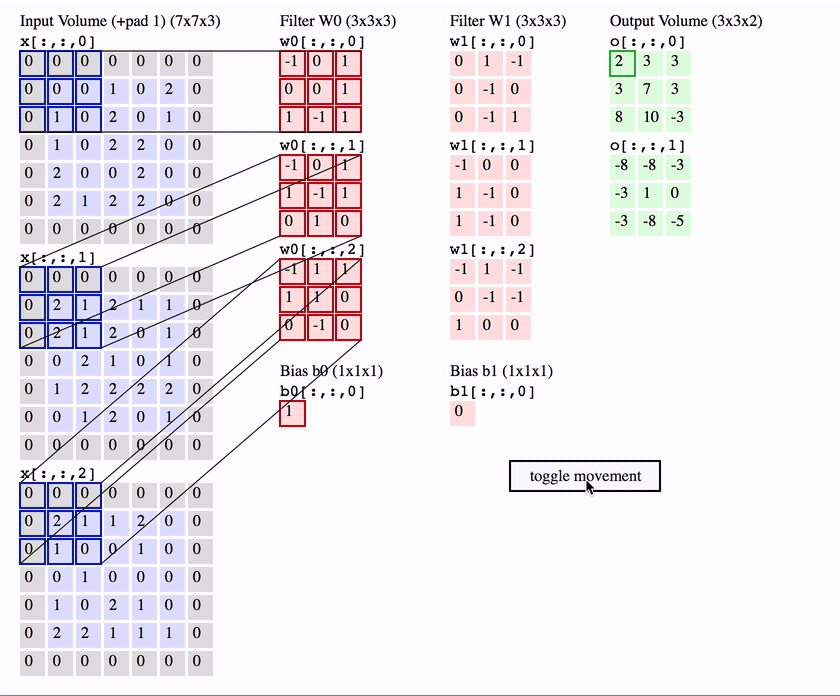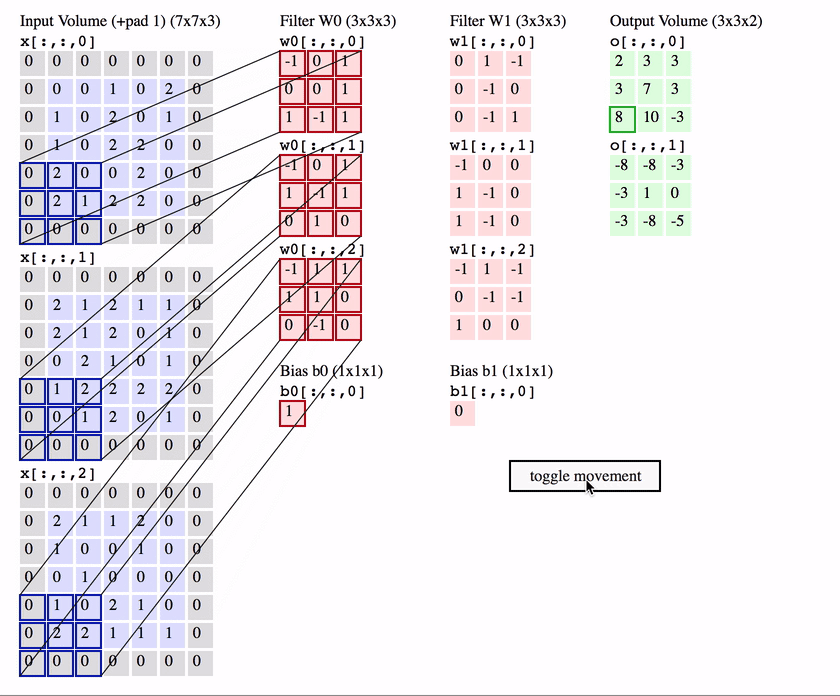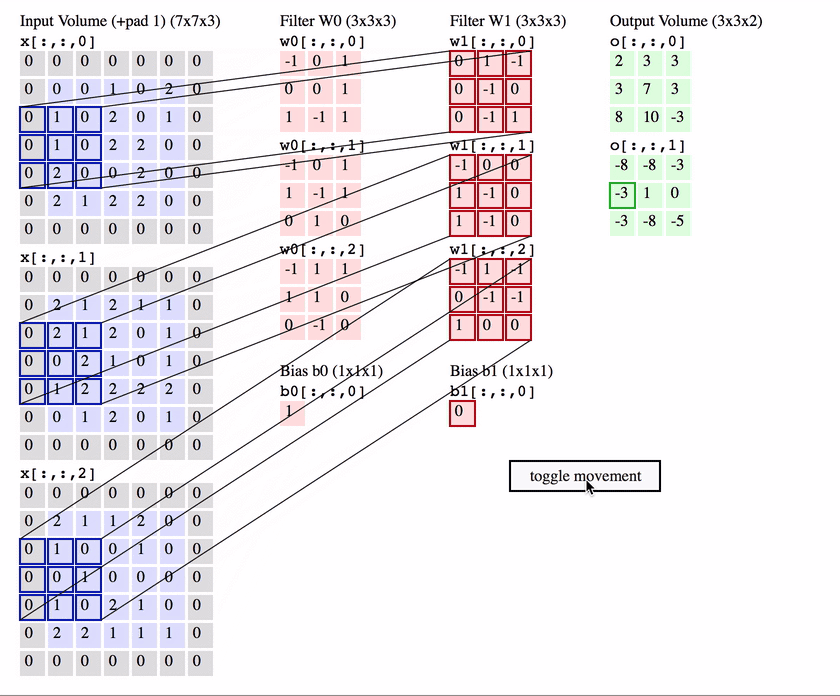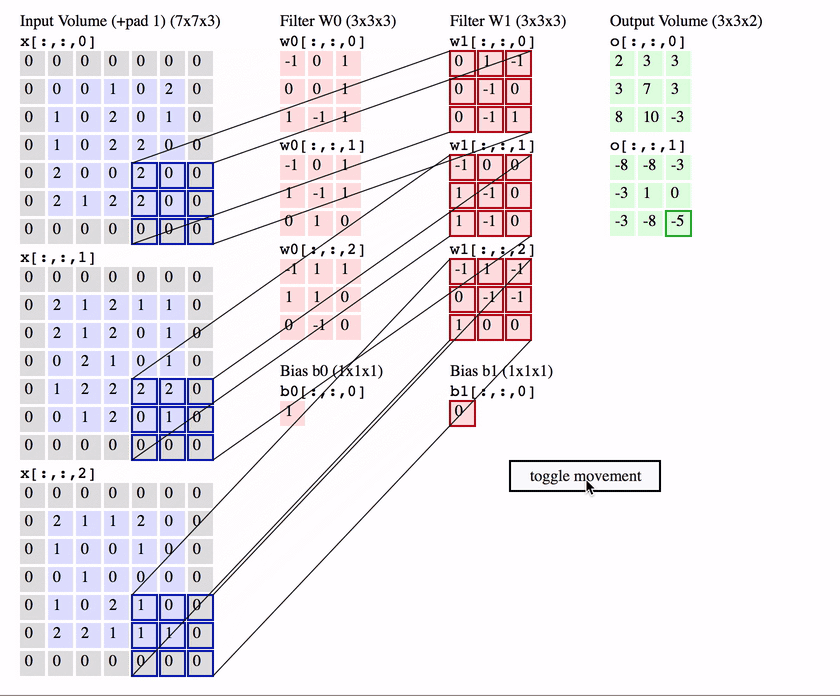
3.3 Transltion invariance & Translation equivariance
- Translation invariance(불변성)와 Translation equivariance는 서로 상반되는 개념
- Translation invariance: 물체의 입력 내 시/공간 상 절대적 위치가 함수 출력에 영향 미치지 않음
- Translation equivariance: 물체의 입력 내 시/공간 상 절대적 위치가 함수 출력에 영향 미침
- 이미지 데이터 이용한 머신러닝 task는 물체의 절대적 위치는 고려하지 않음과 동시에 물체간 상대적 위치 고려해야 함
- CNN모델의 경우, convolution 연산의 translation equivariance 특성에 파라미터 공유를 함으로써 translation invariance 특성 또한 갖는 것
(1) Translation invariance
- 입력 위치가 변해도 출력은 변하지 않음
- 이미지 상에서 사물의 위치가 다르더라도 출력 값은 동일하다는 의미
- Max-pooling이 대표적인 translation invariance 함수
- 여러 픽셀 중 최댓값 지닌 픽셀 출력 하나를 출력하기에 서로 다른 [1,0,0]과 [0,0,1]을 넣어도 출력 결과로는 1이라는 동일한 결과 도출
- 아래 그램에서 석상의 위치(왼쪽, 중앙, 오른쪽)에 상관 없이 똑같이 동일한 출력값 생성(석상)

(2) Translation Equivariance
- Equivariance는 variance, 즉 가변성 의미
- 입력 위치 변함에 따라 출력값 변함
- 아래 얼굴 이미지 통해 translation equivariance 이해할 수 있음
- (왼쪽) Not Face의 경우에도 눈 2개, 코 1개, 귀 2개, 입 1개로 구성되어 있음
- 하지만, 왼쪽 그림은 얼굴로 보기에는 상대적 위치가 맞지 않기에 일반적으로 얼굴로 보지 않음

(3) Translation Equivariance -> Translation invariance in CNN
- 아래 그림은 CNN의 translation invariance 특성 보여줌
- 파란색: 이미지
- 초록색: Convolution layer의 Feature map
- 노란색: 더 깊은 Convolution layer의 Feature map
- 파란색 이미지 하단 왼쪽에 눈과 코가 있다고 가정
- 초록색 Feature map에서는 눈 채널, 코 채널 각각 하단 왼쪽의 눈, 코 위치 따라 활성화 값 출력
- 노란색 Feature map에는 face 채널, leg 채널 등이 있는데 이전 feature에서 크게 활성화된 하단 왼쪽 영역의 눈. 코 채널을 합쳐서 face 채널의 하단 왼쪽 영역에 큰 활성화 값 출력됨
- 여기까지는 각 입력에서 특징 위치와 동일하게 출력이 되었기에 Translation Equivariance 하다고 할 수 있음
- 하지만, FCN 거쳐 마지막 label 확률 벡터 출력하는 부분에서는 위치와 상관없이 human body가 나오므로 translation invariant 하다고 할 수 있음

- 위 이미지와 동일하지만, 사진에서 눈과 코의 위치가 상단 왼쪽에 있음
- 이미지 특징의 위치가 서로 상이한데 human body라는 동일한 출력값 내놓기 때문에 translation invariance하다고 할 수 있음

- 즉, 이미지 상에서 객체가 어느 위치에 있든 label 확률값은 동일하게 출력하기 때문에 Convolution 연산의 equivariance한 특성 + 파라미터 공유하기에 translation invariant한 특성 가짐
04. 딥러닝에서의 Inductive Bias
- Inductive Bias는 크게 Relational Inductive Bias와 Non-relational Inductive Bias 2개로 나뉨
- Relational Inductive Bias는 관계에 초점 맞춘 것. 입력 Element와 출력 Element 간의 관계 의미
- 딥러닝 모델에는 다양한 기본 구조들이 존재함
- 가장 단순하면서도 기본적인 구조라고 할 수 있는 Fully Connected Network(FCN), 이미지 다루는 분야에서 많이 사용되는 Convolutional Neural Network(CNN), 언어를 비롯한 시계열 데이터에서 효과적인 Recurrent Neural Network(RNN) 등이 가장 널리 알려진 구조들
- CNN 가정? 해당 pixel은 인접한 pixel들과 깊은 연관 가지고 있음
- RNN 가정? 현재 시점과 더 가까운 거리 가지는 sequence 요소들이 지금 시점에 많은 영향 미칠 것


4.1 Fully Connected Layers
- 입력 Entities가 개별 Unit으로 정의됨
- 서로 모두 연결되어 있는 All-to-all Relations 가짐
- 모든 입력 Element가 출력 Element에 영향 미치기에 구조적으로 특별한 Relational Inductive Bias 가정하지 않음(Weak)
- input에서 output으로 전파되는 과정에서 weight가 각각 독립적이이며 공유되지 않음
4.2 Convolutional Layers
- 입력이 이미지처럼 격자(Grid) 구조로 되어 있음
- 입력 크기보다 작은 Convolutional Filter 사용해 전체의 일부만을 대상으로 Convolution Operation 수행
- CNN은 receptive filed 내 입력들 간의 상관관계만을 모델링하는 필터들로 구성되어 있음
- 이를 통해 전체 입력간 상관관계 모델링하는 FCN과 차별성 지님
- Convolution layer는 local한 특성 추출하는 다수의 filter들로 구성되어 있으며, 각각의 filter는 translation equivariance한 특성 포착
- CNN에 포함된 pooling layer는 translation invariance한 특성 포착
- 동일한 weight 가진 1개의 Convolution Filter 가지고 전체 격자 순회하는 구조(Parameter Sharing)
- Parameter sharing? 각 Local 영역에서 feature 추출하는 필터들 간 파라미터 공유
- 이는 이미지 데이터의 translation invariance/stationarity 특성 활용한 것
- 데이터셋이 특정 위치에 따라 통계적 특징 바뀌지 않음
- Entites 간의 Relation이 지역성 즉 서로 가까운 Element 간에만 존재한다고 가정하는 것
- 결과적으로 어떤 특성을 가지는 Element들이 서로 뭉쳐있는지 중요한 경우에 탁웛ㄴ 구조로 활용 가능
- Filter는 object 위치와 상관없이 특정 패턴 학습
- 위와 같은 특징들을 통해 이미지 데이터셋이 갖는 inductive biases(stationarity, locality, translation invariance, translation equivariance)를 효과적으로 반영함과 동시에 높은 효율성 지님
4.3 Recurrent Layers
- CNN과 유사한 방식으로 작동(공간의 개념 -> 시간의 개념)
- 입력 값들이 시계열 특성 가지는 것으로 가정: 미래의 데이터가 이전 time step의 영향 받음
- 과거의 데이터가 현재에도 영향 미친다는 순차적인 특성(Sequential Relation)을 잘 학습하기 위해 이전 레이어의 결과를 다음 레이어에 활용하는 RNN 구조가 유용하게 활용
- 동일한 순서로 동일한 입력 들어오면 출력이 동일하다는 점에서 Temporal invariance 특성 가짐
05. Inductive bias in Transformer
Vision Transformer 논문은 2020년 발표되었습니다.
논문명: An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale(2020)
발표: Google Research, Brain Team
해당 논문에서 inductive bias는 총 8번 등장하는데요.
등장하는 구절들 중, 핵심적인 부분들을 모아보면 다음과 같습니다.
We note that Vision Transformer has much less image-specific inductive bias than CNNs.
In CNNs, locality, two-dimensional neighborhood structure, and translation equivariance are baked into each layer throughout the whole model.
In ViT, only MLP layers are local and translationally equivariant, while the self-attention layers are global.
The two-dimensional neighborhood structure is used very sparingly: in the beginning of the model by cutting the image into patches and at fine-tuning time for adjusting the position embeddings for images of different resolution (as described below).
Other than that, the position embeddings at initialization time carry no information about the 2D positions of the patches and all spatial relations between the patches have to be learned from scratch.
- Transformer는 Positional Embedding이나 Self-Attention mechanism 통해 모든 정보 활용
- 모든 input 그대로 활용해 attention score 구함
- 하지만, 추가적인 가정(inductive bias)은 부족
- Transformer는 FFN을 확장한 모델로 CNN 대비 상대적으로 적은 inductive bias에 기반
- 높은 표현력 지니나 낮은 sample efficiency 보임
- 이러한 tradeoff 조절하기 위해 vision/speech 분야에서 다양한 연구 진행
- 트랜스포머의 경우, input sequence의 모든 토큰 이용해 연산하는 attention mechanism에 따라 상대적으로 CNN에 비해 inductive bias 약한 편
- 입력 데이터의 모든 요소간의 관계(attention weight) 계산하므로 CNN보다 inductive bias가 적음
ViT 논문에서는 Transformer와 CNN의 성능 비교하며 다음과 같이 결론을 내고 있습니다.
"This result reinforces the intuition that the convolutional inductive bias is useful for smaller datasets, but for larger ones, learning the relevant patterns directly from data is sufficient, even beneficial."
이후에는, ViT가 갖는 한계점들을 극복하기 위한 다양한 시도들이 있었는데요.
이러한 다양한 시도들은 아래와 같습니다.
5.1 DeiT
논문명: Training data-efficient image transformers & distillation through attention(2020)
발표: Facebook AI

- 적은 수의 파라미터와 간단한 컴퓨팅 자원, 효율적인 수의 데이터 만으로 성능 향상
- Knowledge Distillation 아이디어 활용해 token-based Distillation(ViT의 class token과 유사) 방식 적용
- Data augmentation 활용하여 적은 양의 데이터로도 학습시킬 수 있음
5.2 ConViT
논문명: ConViT: Improving Vision Transformers with Soft Convolutional Inductive Biases(2021)
발표: FacebookAI

- CNN의 장점 + Transformer 장점 결합해 "Soft Inductive Bias" 개념 활용
- GPSA(Gated Positional Self-Attention) 활용해 Relative Self-Attention을 초기화해 Convolution의 효과를 냄
5.3 Swin Transformer
논문명: Swin Transformer: Hierarchical Vision Transformer using Shifted Windows(2021)
발표: Microsoft Research Asia
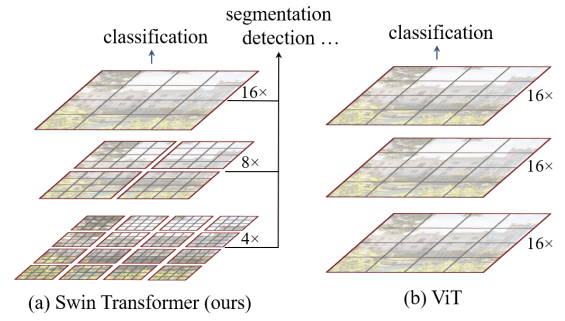
- Hierarchical한 Local window와 패치 적용
- 전체 영역이 아닌 window 안에 포함된 패치들 간의 self attention 계산해 locality inductive bias 개입
5.4 CMT
논문명: CMT: Convolutional Neural Networks Meet Vision Transformers(2021)

- Long Range에 강력한 Transformer와 Feature Map 통한 Local Feature에 강력한 CNN 장점 결합
- LPU(Local Perception Unit) 방식 활용해 Depth Wise Convolution을 3x3로 진행하여 Locality 정보 추출해내고 Residual 더해줌
참고
머신러닝에서의 Bias와 Variance
CNN의 inductive bias
What is inductie bias?
CNN의 stationarity와 locaility
CNN과 이미지가 찰떡궁합인 이유
논문 제목: Relational Inductive Biases, Deep Learning and Graph Networks
Relational inductive biases, deep learning, and graph networks(2018)
[Paper Review] ConViT: Improving Vision Transformers with Soft Convolutional Inductive Biases
'Tool' 카테고리의 다른 글
| [Messaging System] MQ vs Kafka 정리 (0) | 2025.03.14 |
|---|---|
| [Lilys AI] AI vs 사람, 누가 더 요약을 잘할까? (4) | 2024.05.02 |
| MLX, 애플에서 발표한 오픈 소스 딥러닝 프레임워크 (2) | 2023.12.26 |
| PEFT(효율적 파라미터 파인 튜닝) 활용한 성능 최적화: 프롬프트 튜닝 딥다이브 (0) | 2023.12.13 |
